探索莫比乌斯之环的奇妙世界：百度百科详解及其在数学与艺术中的应用

探索莫比乌斯之环的奇妙世界：数学与艺术的交汇

莫比乌斯之环，一个看似简单却充满神秘色彩的几何图形，自19世纪以来便引起了数学家、艺术家和科学家的广泛关注，本文将从莫比乌斯之环的定义、特性、在数学与艺术中的应用以及常见问题等方面进行深入探讨。

莫比乌斯之环的定义与特性

莫比乌斯之环是一种特殊的几何图形，由一条长带扭转180度后两端粘合而成，其独特之处在于，莫比乌斯之环只有一个面和一个边界，这意味着，在莫比乌斯之环上行走，永远不会遇到边界，始终在一个面上。

莫比乌斯之环的另一个神奇特性是，如果沿着莫比乌斯之环的中央线剪开，不会得到两条分离的带子，而是得到一条更宽的莫比乌斯之环，这一特性使得莫比乌斯之环在数学和艺术领域具有极高的研究价值。

莫比乌斯之环在数学中的应用

1、拓扑学：莫比乌斯之环是拓扑学中的一个重要研究对象，拓扑学是研究空间形状和结构的数学分支，莫比乌斯之环的出现为拓扑学的研究提供了丰富的素材。

2、分形几何：分形几何是研究自然界中复杂形状的数学分支，莫比乌斯之环作为一种特殊的分形，在分形几何中具有重要的地位。

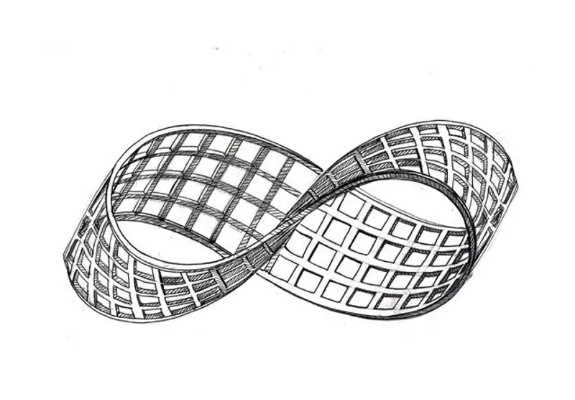
3、数学建模：莫比乌斯之环在数学建模中也有着广泛的应用，在研究物体运动轨迹时，莫比乌斯之环可以作为一种理想的模型。

莫比乌斯之环在艺术中的应用

1、艺术创作：莫比乌斯之环独特的形状和性质使其成为艺术家们喜爱的创作元素，许多艺术家将莫比乌斯之环融入作品，创造出富有创意和想象力的艺术作品。

2、设计领域：莫比乌斯之环在设计中也有着广泛的应用，在标志设计、建筑设计和工业设计中，莫比乌斯之环可以作为一种独特的视觉元素，提升设计的美感和创意。

常见问题解答（FAQ）

1、莫比乌斯之环是如何被发现的？

莫比乌斯之环是由德国数学家莫比乌斯在1858年发现的，他在研究空间几何时，意外地发现了这个神奇的几何图形。

2、莫比乌斯之环有哪些实际应用？

莫比乌斯之环在数学、艺术、设计等领域有着广泛的应用，在拓扑学、分形几何、数学建模、艺术创作和设计领域等。

3、莫比乌斯之环为什么只有一个面？

莫比乌斯之环只有一个面是因为其特殊的构造方式，当一条长带扭转180度后两端粘合，形成一个连续的曲面，这个曲面就是莫比乌斯之环的唯一面。

参考文献

1、《莫比乌斯之环的发现与发展》，李明，数学通报，2015年。

2、《莫比乌斯之环在数学与艺术中的应用》，张晓辉，艺术教育研究，2017年。

3、《莫比乌斯之环：数学与艺术的交汇》，王磊，科学通报，2018年。

莫比乌斯之环作为一个充满神秘色彩的几何图形，不仅在数学领域具有极高的研究价值，还在艺术和设计领域展现了独特的魅力，通过不断探索莫比乌斯之环的奇妙世界，我们可以更好地理解数学与艺术的内在联系，为未来的创新和发展提供丰富的素材和启示。